고정소수점과 부동소수점의 이해
이전 글에서 제시된 float 계산에 등장하는 부동소수점에 의한 오류 코드에 대해 다뤘습니다. 오류가 발생하는 이유를 이해하기 위한 개념이 생각보다 많이 어려웠습니다. 때문에 제 개인적으로 따로 다루는 것이 개인에게 좋을 것이라 판단해 정수 자료형에서 사용하는 고정소수점과 실수 자료형에서 사용되는 부동소수점의 특징과 개념에 대해 따로 적어보겠습니다.
- 고정소수점(fixed point): 소수점의 위치가 고정된 상태로 실수를 정수와 같은 방법으로 처리되는 방식을 말합니다. 때문에 다룰 수 있는 범위가 제한적입니다.
- 부동소수점(floating point): 위의 이유로 컴퓨터에서 광범위의 수를 다루기 위해 만들어진 실수를 처리하는 방식으로 정수부를 0이 아닌 한 자리로 이동해서 표현하는 '정규화'를 거치는 방식입니다. 이 방식은 IEEE 754라는 국제 표준을 따릅니다.
- IEEE 754란? IEEE에서 개발한 컴퓨터에서 부동소수점을 표현하는 가장 널리 쓰이는 표준입니다.
둘의 차이는 고정소수점은 정수부 / 소수부, 부동소수점은 지수부 / 가수부로 분류되고 정규화 사용 유무이다. 정규화를 거치는 부동소수점은 2진수로 변환하려는 소수점 포함 전체를 2진수로 한 번에 표현하는 걸로 시작합니다. 때문에 소수 부분의 계산 방식에서 차이가 있습니다. 고정소수점은 나누기로, 부동소수점은 곱하기로 계산하는 게 좋습니다. 그리고 컴퓨터는 더 넓은 범위의 많은 수를 저장하고 다룰 수 있기 위해 소수점의 위치를 바꿀 수 있는 방식인 부동소수점을 사용하는 겁니다.
고정소수점부터 먼저 다루겠습니다.
| 0 | < | > | < | > |
표로 알아보기 쉽도록 표현했습니다. 이제 예시로 10.31을 고정 소수점으로 지정해 10진수를 2진수로 변환해봅시다.
위의 표는 2byte, 16bit로 왼쪽부터 1bit 부호비트 / 2~8 (7bit) 정수부 / 9~16(8bit) 소수부로 나뉩니다. 부호비트는 양수이니 0을 넣고 시작합니다. 10.31의 계산을 그림판으로 써봤습니다.
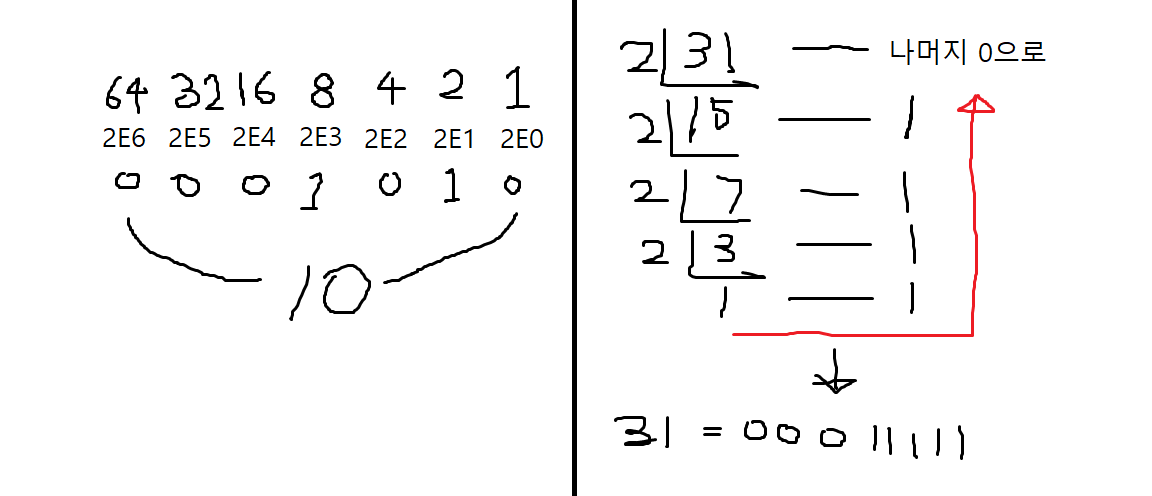
그림표로 보기 쉽게 계산했습니다. 이에 따라 표를 작성합니다.
| 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
부동소수점을 설명하기 전 정규화에 대해 먼저 설명하겠습니다. 정규화는 정수부를 0이 아닌 한 자리로 이동해서 표현하는 방식입니다. 10진수로 예시로 들겠습니다.
- 123.456 ----<정규화>----> 1.23456 * 10E2 (1.23456을 가수부(m), 23이 소수점 뒤로 간 만큼 10의 2 거듭제곱으로 표현, 여기서 2승을 지수부(e)라고 부릅니다.)
- 0.00368 ----<정규화>----> 3.68 * 10E-3 (3.68을 가수부(m), 368이 정수부로 간 만큼 10의 -3거듭제곱으로 표현, 여기서 -3승을 지수부(e)라고 부릅니다.)
10진수로 개념을 알아봤습니다. 이제 2진수입니다. 부동소수점을 사용하는 실수 자료형은 float, double, long double이 있는데 4byte(32bit), 8byte(64bit)를 다루며 그들의 가수부, 지수부 할당입니다.
- 32bit(float): 부호 1bit / 지수부(e) 8bit / 가수부(m) 23bit / bias 127: 127초과 표기법 (IEEE 754표준)
- 64bit(double): 부호 1bit / 지수부(e) 11bit / 가수부(m) 52bit / bias 1023: 1023초과 표기법 (IEEE 754표준)
bias는 지수 저장 공간에 음의 지수와 양의 지수를 표현하기 위해 선택한 숫자로 8bit의 0~255의 절반값인 127을, 11bit - 0~2047의 절반값인 1023이 된 것입니다. 이와 관련된 이론에는 'excess-127 code' 라는 것이 사용되었다고 하는데 이것까진 너무 깊게 들어가는 것 같아 생략하겠습니다.
이제 float기준으로 50.625를 2진수 부동소수점으로 표현하겠습니다. 양수이므로 부호비트 0으로 시작합니다.
| 0 | < | > | < | > |

위의 계산에서 지수부만 구해봅시다. 5+127은 132, 132를 2진수로 표현하면 10000100 (2E7+2E2)
이제 각자의 위치로 이동하여 표를 채우고 나머지 빈칸엔 모두 0으로 채웁니다.
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
이렇게 표현이 됩니다. 제일 처음으로 돌아갑시다.

어라? 값의 오류가 있다 했는데 50.625는 딱 표현이 되는데? 그럼 정확하게 표현이 되는 건데 그럼 값의 오류가 생길 이유가 없지 않음?

팍씨! 프로그래머 초보 티 엄청 내네 ㅋㅋㅋ
라고 생각하면 안 되더라고요 ㅋㅋ... 50.625는 딱 맞아떨어지는 수이기 때문에 딱히 문제없지만 32bit, 64bit를 넘어서도 표현할 수 없는 무한소수로 표현되는 값이 있습니다. 0.1f를 컴퓨터 방식인 부동소수점으로 2진수로 표현해 보겠습니다.
| 0 | < | > | < | > |

0.1의 부동소수점의 2진수는 아래와 같다.
| 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
가수 부분이 끝나지 않고 32bit를 넘어선 이후는 표현하지 않고 나머지를 오차로 지정합니다. 그렇기 때문에 아래의 코드
float = 0.1f 에서 초기값인 0.1f는 0.1과 비슷한 수이지 정수처럼 딱 0.1로 정의하고 있지 않습니다.
프로그래머 초보이고 IEEE와 bios, 정규화 등이 생겨난 배경 등을 자세히 공부하지 않고 문법, 약속만 알려고 하니 많이 헷갈렸지만, 왜 오차가 발생하는지 이해를 할 수 있었습니다. 그러니, 실수를 다루는 작업, 코드를 다룰 때는 항상 주의해서 짜야겠다는 생각을 하게 되었습니다.
끝